算法:

1.将依赖集F的右侧分解为只有一个属性

2.去掉冗余项:从第一个函数依赖X -> Y开始，假设将其从F中去掉（从F里面删除，不去推导他的关系，如果删除成立，下一次求闭包也不能算他的关系，是真正意义上的删除），然后在剩下的函数依赖 中求X的闭包，看Y是否属于X的闭包中，如果属于，则去掉X->Y依赖，不属于，则保留（重新加入回来）。直到扫描完所有的函数依赖为止。

3.去掉冗余属性:选取左边属性个数大于1的所有依赖，假设为XY->A， 判断方法如下，假设删除属性 X,计算Y的闭包，判断A是否属于Y的闭包，如果属于，则删除X，同理计算Y。（这边的删除是不从F里面删除的，如果求闭包，能推出假设删除的属性，那也还能用）

注:若(3) 中改变了函数依赖F，则需要重新做一次步骤(2)

例： R={A,B,C,D,E,G}，F={B→D,DG→C,BD→E,AG→B,ADG→BC}，求F的最小函数依赖

解：

1、运用分解律

进行拆除F={B→D,DG→C,BD→E,AG→B,ADG→B,ADG→C}

2、判断冗余的函数依赖

1.假设删除B→D，则B+={B}，故保留

2.假设删除DG→C，则(DG)+={D,G}，故保留

3.假设删除BD→E，则（BD)+={B,D}，故保留

4.假设删除AG→B，则（AG)+={A,G}，故保留

5.假设删除ADG→B，则(ADG)+={A,D,G,C,B,E}，有B，删除

6.假设删除ADG→C，则（ADG)+={A,D,G,B,E,C}，有C，删除

综上，F更新为F={B→D,DG→C,BD→E,AG→B}

3、判断左侧的冗余属性

DG→C,BD→E,AG→B，左侧的属性个数大于1，故进行判断是否冗余

1.看DG→C，假设删除D，则G+={G}，假设删除G，则D+={D}，无C，保留

2.看BD→E，假设删除B，则D+={D}，假设删除D，则B+={B，D，E}，有E，则删除D，得到B→E

3.看AG→B，假设删除A，则G+={G}，假设删除G，则A+={A}，无B，保留。

综上，F更新为F={B→D,DG→C,B→E,AG→B}

4、由于步骤3更新了F，故在进行一次步骤2

1.假设删除B→D,显然B的闭包不包含D

2.假设删除DG→C，显然DG的闭包不包含C

3.假设删除B→E，显然B的闭包不包含E。

4.假设删除AG→B，显然AG的闭包不包含B。

综上所述最小依赖集为F={B→D,DG→C,B→E,AG→B}。

注：最小依赖集不唯一。

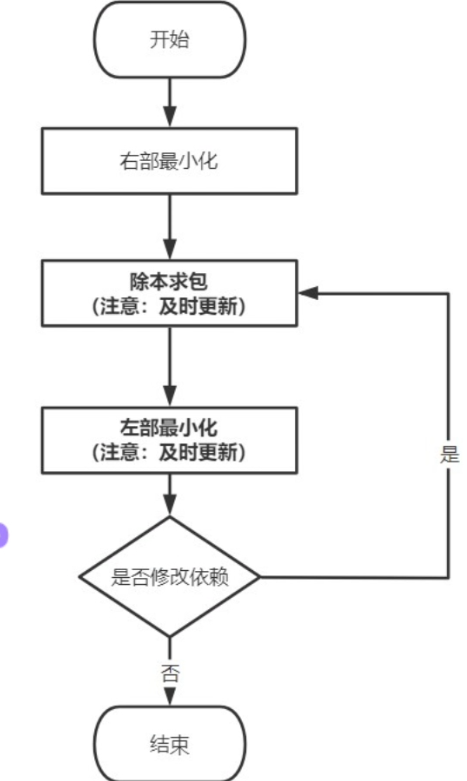
流程图