
动测量,这些数据主要分为时序数据和事件数据两大类。时序数据指的是实值-时间序列(通常有固定的时间间隔),例如CPU使用率等;而事件数据指的是记录了特定事件发生的序列,例如内存溢出事件等。为了保证产品的服务质量、减少服务宕机时间,从而避免更大的经济损失,对关键的服务事件的诊断显得尤为重要。实际的运维工作中,对服务事件进行诊断时,运维人员可以通过分析与服务事件相关的时序数据,来对事件发生的原因进行分析。虽然这个相关关系不能完全准确的反映真实的因果关系,但是仍然可以为诊断提供一些很好的线索和启示。
那么问题来了,如何自动的判断事件和时序数据的关联关系呢?
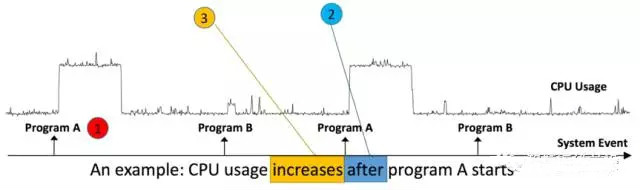
本文中,作者将事件(E)和时序(S)数据相关关系问题转化为两样本问题(two-sample problem),并使用邻近算法(nearest neighbor method)判断是否相关。主要回答了三个问题:A.E和S之间是否存在相关关系?B.若存在相关关系,E和S的时间先后顺序是什么?E先发生,还是S先发生?C.E和S的单调关系。假设S(或者E)先发生,S的增加还是降低导致的E发生?如图,事件为程序A和B的运行,时序数据为CPU使用率。可以发现,事件(程序A的运行)与时序数据(CPU使用率)存在相关关系,并且是程序A运行后CPU使用率发生升高的变化。
文章的算法架构主要分为三部分,来分别解决相关性、时间先后顺序和单调性三个问题。接下来将对这三个部分进行详细介绍。
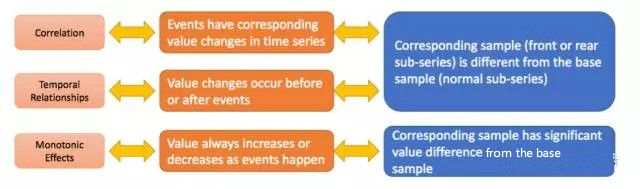
文章将相关性的判断转化为两样本问题,两样本假设检验的核心是判断两个样本是否来自相同的分布。首先选取事件发生前(或者后)对应的N段长为k的时序样本数据,用A1表示。样本组A2则是在时间序列上随机选取一系列长度为k的样本数据。样本集为A1并上A2。如果E和S相关,则A1和A2的分布不同,否则分布相同。怎样来判断A1和A2的分布是否相同?我们看下面这个例子:
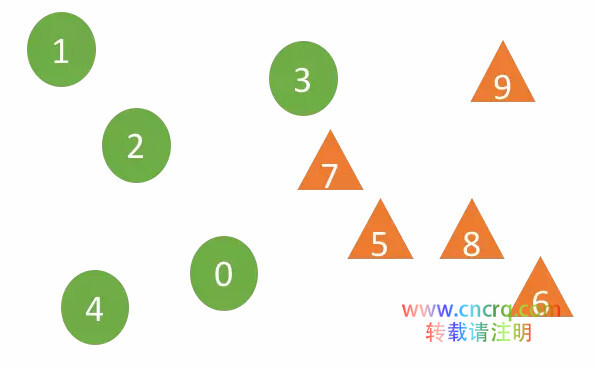
上图中样本0-4来自样本组A1,5-9属于样本组A2,使用DTW算法来计算两个样本之间的距离(DTW算法可以很好的适应序列数据的伸缩和位移)。某个属于样本组Ai(i=1或2)的样本X,对于X的r个最近邻居样本,与X属于相同样本组的个数越多则意味着样本组A1和A2分布更不同,即E和S越相关。例如,取邻居个数r=2,样本7的两个最近邻居分别是来自两个不同样本组的3和5,但是样本5的两个最近邻居是来自相同样本组A2的7和8。文章使用置信系数(Confident coefficient)来判断“假设检验H1”(两个分布不相同,即E和S相关)的可信度,置信系数越大,H1越可信。算法的两个关键参数:最近邻居个数r和时间序列长度k,邻居个数为样本个数的自然对数,时序数据的自相关函数曲线的第一个峰值为序列长度。
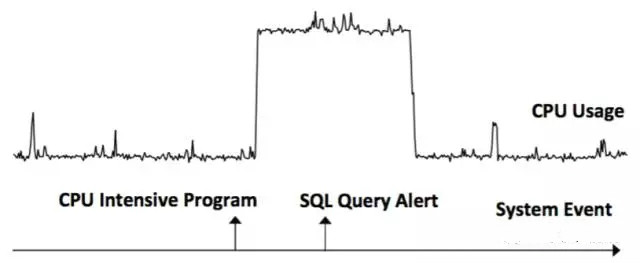
选取事件发生前后的序列与随机选取的时间序列求相关性,结果为Dr和Df。如果Dr为True,Df为False,代表E的发生先于S的发生(E -> S)。如果Dr为False,Df为True,或Dr为True,Df为True,代表S的发生先于E的发生(S -> E)。如下图例子,事件CPU Intensive Program –> 时序数据CPU Usage,时序数据CPU Usage -> 事件SQL Query Alert。
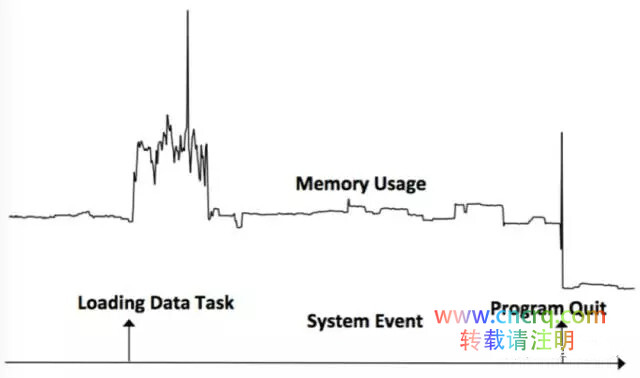
单调性由事件发生前后时间序列的变化来判断,如果事件发生后的时间序列比之前的序列取值要大,单调性为增加,否则为降低。如下图所示事件loading Data Task导致了Memory Usage的增加,事件Program Quit导致了Memory Usage的降低。
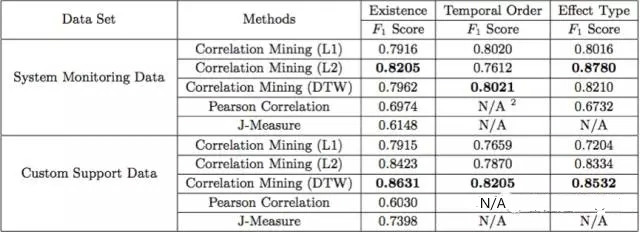
文章通过使用微软的系统监控数据和客服团队的数据对算法性能进行验证,数据分别是24个 S(内存、CPU和DISK数据)和52个 E (特定任务的执行),7 个S(HTTP状态码)和57个 E (服务主题),评价标准为F-score。结果表明DTW距离比其他的距离(L1和L2)整体表现更好,算法整体比两个baseline算法(皮尔森相关和J-Measure)表现要好。
文章介绍了一套全新的无监督的方法研究事件和时序数据的关系,回答了三个问题:E和S是否相关?E和S发生的先后顺序?以及单调关系是什么?相比较现在很多的相关关系研究,主要是事件之间的关联关系和时序数据之间的关联关系,本文则侧重事件和时序数据间的关系,是第一个回答了事件和时序数据间上述三个问题的工作。
事件诊断一直是运维领域一个很重要的工作,事件和时序数据的相关性不仅可以为事件诊断提供很好的启发,而且在帮助进行根因分析等都能提供很好的线索。作者在微软的内部数据集上对算法做了验证,并取得了很好的效果,这对于学术和工业届都有很高的价值。


