Python动态规划实现虚拟机部署

本文章为个人拙见，仅仅提供参考，不一定正确，各位大佬可以发表自己的意见。

考虑到在虚拟机部署中资源提供商通常希望自己的收益最大化，现假设有一台宿主机，共有x个cpu和y GB的内存，用户可以采取自己报价的方式向资源提供商申请使用虚拟机资源，譬如说付w元申请a个cpu和b GB内存的一台虚拟机。请你设计一个算法，让资源提供商可以合理地安排虚拟机，使得自己的收益最大化。

输入：
n x y
2 4 200
4 2 150
…

说明，n表示共有n条用户报价申请，宿主机共有x个cpu和y GB的内存；

以下n行，每行表示用户申请的cpu和内存数，以及用户报价的金额。

该问题为寻找全局最优解问题，采用动态规划的思想。找最大利益是最终的问题，可以将最大利益的子问题看做是已经报价的每个用户最大金额，并将其所要求的CPU数和内存数加入到总的需求总，与提供的CPU数和内存容纳进行对比。解决了目前最大报价的用户，下一个最大报价又可以看做是一个子问题，但CPU和内存容量需要减去已经分配的，如此反复，到CPU和内存容量不能满足任何一个用户要求为止，最优解便求得。

运行结果:

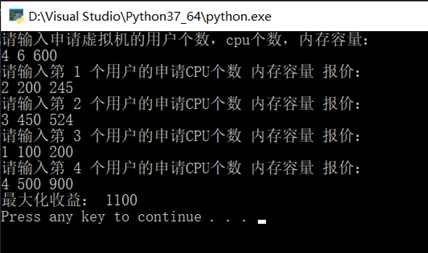
源代码

import sys
print("请输入申请虚拟机的用户个数，cpu个数，内存容量：")
a = list(map(int, input().split()))  # 用数组a来存储参与报价的用户的个数,云端要存储的cpu个数，容量大小
a1 = a[0]  # 存储用户个数，要输入几行数据
a2 = a[1]  # 存储cpu的个数
a3 = a[2]  # 存储容量
b = []
cpu_num=0
size_num=0
money=0
b1 = [0]*a1  #数组b1存储用户报价
p1 = [0]*a1  #数组p1记录报价金额的位置
for i in range(a1):
print("请输入第",i+1,"个用户的申请CPU个数 内存容量 报价：")
b.append(list(map(int, input().split())))
for k in range(a1):
b1[k] = b[k][2]
p1[k] = k
for i in range(0,a1-1):
for j in range(1,a1-i):
if b1[j]>b1[j-1]:
temp=b1[j-1]
b1[j-1]=b1[j]
b1[j]=temp
temp=p1[j-1]
p1[j-1]=p1[j]
p1[j]=temp
def Fun(i):
global cpu_num,size_num,money
cpu_num=cpu_num+b[p1[i]][0]
size_num=size_num+b[p1[i]][1]
money=money+b[p1[i]][2]
if cpu_num>a2 or size_num>a3:
money=money-b[p1[i]][2]
cpu_num=cpu_num-b[p1[i]][0]
size_num=size_num-b[p1[i]][1]
for i in range(a1):
Fun(i)
print("最大化收益：",money)

到此这篇关于Python动态规划实现虚拟机部署的文章就介绍到这了